宜昌市中考数学试题解析(4)

时间：2024-09-12 09:41:12 学人智库我要投稿

相关推荐

宜昌市中考数学试题解析(4)

　　∵四边形ABCD是菱形，

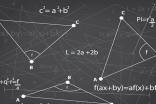
宜昌市中考数学试题解析(4)

　　∴AB∥CD，AC⊥BD，

　　∴∠AEB=90°.

　　又∵∠FDE=90°，

　　∴∠AEB=∠FDE，

　　∴AC∥DF，

　　∴四边形FACD是平行四边形;

　　(3)①连接GE，如图.

　　∵四边形ABCD是菱形，∴点E为AC中点.

　　∵G为线段DC的中点，∴GE∥DA，

　　∴∠FHI=∠FGE.

　　∵EF是⊙O的直径，∴∠FGE=90°，

　　∴∠FHI=90°.

　　∵∠DEC=∠AEB=90°，G为线段DC的中点，

　　∴DG= GE，

　　∴ = ，

　　∴∠1=∠2.

　　∵∠1+∠3=90°，∠2+∠4=90°，

　　∴∠3=∠4，

　　∴FD=FI;

　　②∵AC∥DF，∴∠3=∠6.

　　∵∠4=∠5，∠3=∠4，

　　∴∠5=∠6，∴EI=EA.

　　∵四边形ABCD是菱形，四边形FACD是平行四边形，

　　∴DE= BD=n，AE= AC=m，FD=AC=2m，

　　∴EF=FI+IE=FD+AE=3m.

　　在Rt△EDF中，根据勾股定理可得：

　　n2+(2m)2=(3m)2，

　　即n= m，

　　∴S⊙O=π( )2= πm2，S菱形ABCD= 2m2n=2mn=2 m2，

　　∴S⊙O：S菱形ABCD= .

　　点评：本题主要考查了菱形的性质、圆周角定理、平行四边形的判定与性质、直角三角形斜边上的中线等于斜边的一半、三角形中位线定理、等角的余角相等、等角对等边、平行线的性质、勾股定理、圆及菱形的面积公式等知识，综合性强，证到IE=EA，进而得到EF=3m是解决第3(2)小题的关键.

　　24.(12分)(2015宜昌)如图1，B(2m，0)，C(3m，0)是平面直角坐标系中两点，其中m为常数，且m>0，E(0，n)为y轴上一动点，以BC为边在x轴上方作矩形ABCD，使AB=2BC，画射线OA，把△ADC绕点C逆时针旋转90°得△A′D′C′，连接ED′，抛物线y=ax2+bx+n(a≠0)过E，A′两点.

　　(1)填空：∠AOB=　45　°，用m表示点A′的坐标：A′(　m　，　﹣m　);

　　(2)当抛物线的顶点为A′，抛物线与线段AB交于点P，且 = 时，△D′OE与△ABC是否相似?说明理由;

　　(3)若E与原点O重合，抛物线与射线OA的另一个交点为点M，过M作MN⊥y轴，垂足为N：

　　①求a，b，m满足的关系式;

　　②当m为定值，抛物线与四边形ABCD有公共点，线段MN的最大值为10，请你探究a的取值范围.

　　考点：二次函数综合题..

　　专题：综合题.

　　分析： (1)由B与C的坐标求出OB与OC的长，根据OC﹣OB表示出BC的长，由题意AB=2BC，表示出AB，得到AB=OB，即三角形AOB为等腰直角三角形，即可求出所求角的度数;由旋转的性质得：OD′=D′A′=m，即可确定出A′坐标;

　　(2)△D′OE∽△ABC，理由如下：根据题意表示出A与B的坐标，由 = ，表示出P坐标，由抛物线的顶点为A′，表示出抛物线解析式，把点E坐标代入整理得到m与n的关系式，利用两边对应成比例且夹角相等的三角形相似即可得证;

　　(3)①当E与原点重合时，把A与E坐标代入y=ax2+bx+c，整理即可得到a，b，m的关系式;

　　②抛物线与四边形ABCD有公共点，可得出抛物线过点C时的开口最大，过点A时的开口最小，分两种情况考虑：若抛物线过点C(3m，0)，此时MN的最大值为10，求出此时a的值;若抛物线过点A(2m，2m)，求出此时a的值，即可确定出抛物线与四边形ABCD有公共点时a的范围.

　　解答：解：(1)∵B(2m，0)，C(3m，0)，